Systems In Action
Forces
Forces are a push or pull acting on an object. Forces are what is called a vector quantity. A vector has both a number value as well as a direction. Both the value of the force as well as its direction are fundamentally defining in its effect on the object. A push or a pull may have significantly different outcomes on the object. Direction matters as well as magnitude of the force.
Forces come in two general types:
a) Contact forces: Contact forces act my direct touch. One object/material must directly touch the other to pass on the force. A hammer hitting a nail, a wave crashing into the shoreline, a baseball hitting the catcher’s glove are all examples of contact forces.
b) Action-at-a-distance forces (I prefer the term non-contact forces) do not require physical contact to exert their effect. Magnetism and gravity are examples of forces acting without direct, physical contact between objects or materials.
Mass: Mass is the amount of material of an object. It is what creates and responds to gravity. The mass of any object attracts the mass of any other object by a force (caused by gravity) that is proportionate to each mass and diminishes by the distance that separates the mass. In other words, the further the two objects are apart, the lower the gravitational pull, and the larger each of the masses is, the greater the gravitational pull. Mass is independent of location. An object does not all of a sudden have less material because we bring it to the Moon or outer space. Mass is measured in grams (g). We often use this measure of mass to describe weight which from a scientific stand point is wrong.
Weight: Weight is the actual force that is caused by gravity. As such, it increases and decreases according to changes in the gravitational field that an object is placed in. An object that weighs 600N (roughly the force caused on 60Kg of mass) on Earth would only weigh 100N on the Moon due to its lesser gravitational field. Weight on earth even can change by a tiny fraction if we move an object to great heights. Remember that the force due to gravity (weight) changes with distance of the two objects from one another. If we move an object further from Earth’s surface, the gravitational pull on the object diminishes by a microscopic (but not zero) amount.
Newton’s 2nd Law: The second of Newton’s three great laws allows us to actually quantify (calculate) the relationship of force due to gravity, mass and the gravitational field around an object. Its normal form is: Force = Mass x Acceleration, or F = m x a
In our special case where we calculate the force due to gravity we replace “a” (acceleration) with g (acceleration due to gravity), a constant that has been experimentally determined to be 9.8 m/s2. Our new formula then is:
Forcedue to gravity = Mass x Accelerationdue to gravity, or F = m x g
How do we use this now?
Lets calculate the weight of a 100Kg stone block on Earth (gEarth = 9.8 m/s2), the Moon (gMoon= 1.622 m/s2) and Mars (gMars= 3.69 m/s2):
Earth: F = m x gEarth , F = 100Kg x 9.8 m/s2
F = 980 N, The weight of the stone block on Earth is 980 N (Newtons)
The Moon: F = m x gMoon , F = 100Kg x 1.622 m/s2
F = 162.2 N, The weight of the stone block on the Moon is 162.2 N
Mars: F = m x gMars, F = 100Kg x 3.69 m/s2
F = 369 N, The weight of the stone block on Mars is 369N
Work and Energy:
Energy is defined as the ability to do work. Work is done when a force moves an object. The metric unit of energy is the Joule (j) named in honour of James Prescott Joule.

When work is done on an object there is a transfer and often transformation of energy. For example, a person is pushing a heavy box across the floor of a workshop. The person converts chemical energy stored in his/her muscles into mechanical/ kinetic energy by making the box move. Both inside the person as well as through friction between the box and the floor chemical and kinetic energy are transformed into heat energy. The important thing is that overall the amount of energy remains constant. The energy that initially was stored in chemical form now has been transformed into heat and motion (kinetic energy) but has neither increased nor decreased. This is the famous First Law of Thermodynamics, sometimes also called “Conservation of Energy”. Energy is neither created nor destroyed, it is simply transformed! Which means that the energy of the universe is finite (meaning limited to a very very very very ……very large amount, but still limited).
Forms of Energy:
While there are a number of different types of energy, sometimes they are lumped into two larger groups: Potential Energy and Kinetic Energy. Think of these two as stored forms of energy (potential energy) and energy due to motion (kinetic energy).
Potential Energy:
Lifting a rock against gravity, stretching a spring or elastic band, moving a charged particle against an electrical potential all create a system that is ready to release energy because we put it artificially into a situation of “stress”; stress that wants to be “relieved”. Letting go of the rock, spring, elastic band or charged particle all results in some movement (kinetic energy) and heat due to friction.
Kinetic Energy:
Kinetic energy is the energy of a system due to the motion of its components. Electricity, sound waves, heat motion and the macroscopic motion of entire objects are all examples of kinetic energy.
Work and Friction:
As we will see later in this unit, friction is always present in the moving parts of our machines and devices. Since friction is created when materials slide past one another it is an ever-present companion of motion and results in the production of heat. Any work that is done inevitably produces some heat due to friction. This means that there is always some loss of energy, no matter how well we construct our mechanical devices. Reducing the loss due to friction is a major concern of mechanics.
Calculating Work:
Work (in joules) = Force (in Newtons) times Distance (in meters)
W = F x d
Example: Josh pushes a box 3 meters and uses 150Newtons of force through these 3 meters. F = 150 N, d = 3m
W =150N x 3m = 450joules
Let’s combine this calculation with our previous calculations involving force:
Josh wants to lift a 25kg box 1.5 meters onto the back of a pickup truck. How much work does he need to do? Before we can answer this we first need to calculate how much force is needed to lift the 25kg box against Earth’s gravity ( creating potential energy by the way!)
Recall that F = mxg
In this case m = 25kg and g= 9.8m/s2
F = 25kg x9.8 m/s2
F = 245 N Josh needs to use 250 Newtons of force to lift the box.
Now we can calculate the amount of work needed:
W = 245N x 1.5m
W = 367.5 joules Josh needs to do 367.5 joules of work on the box to lift it 1.5 meters into the air.
Machines:
machines do all sorts of things for us but ultimately we have machines to make things easier for us. Machines can make things easier for us in three basic ways:
1) Increasing the force that can be applied to an object
2) Decreasing the force needed to move an object (almost the same as 1) but not quite)
3) Changing the direction of a force to be more convenient
Examples:
Using a lever increases the force that we apply to an object. Using a ramp or pulley decreases the force needed to move an object. Using a pulley, even if it doesn’t reduce the amount of force needed, allows us to lift a flag up the flag pole without needing to climb the pole.
Mechanical Advantage:
Mechanical advantage is the result of a machine that changes the amount of force that is produced compared to what is applied. The force that is produced is called the output force and the force that is applied to the machine is called the input force. If the output force is greater that the input force, in other words if we get more from the machine than we put in that is an advantage.
We calculate mechanical advantage (MA) by dividing output force by input force.
MA = output force (Fout) ÷ input force (Fin)
A mechanical advantage of 1 means input and output forces are equal and no advantage is gained. A mechanical advantage of greater than 1 means a real advantage is gained. A mechanical advantage of less than 1 means we are actually looking at a mechanical disadvantage (more force is needed because of the machine than would be necessary without it). This last case seems like it would be of any use but we actually use it regularly, just not to gain a mechanical advantage.
Example Calculations:
A machine creates 500N of output force with an input of 250N. What is the MA?
MA = 500N / 250N = 2
This machine has a mechanical advantage of 2.
Let’s say we want to lift a 40,000N weight using this machine. How much input force would be needed?
MA = 2 = 40,000N / ?
In other words 40,000 divided by what is 2? Try using algebra to find the answer.
It’s 20,000N but prove to me why 🙂
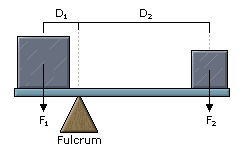
Levers:
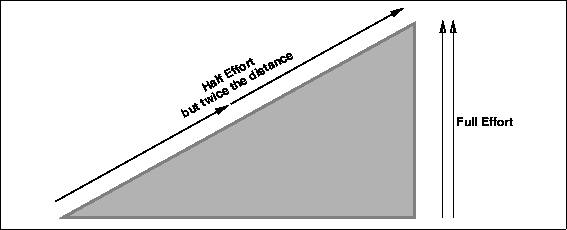
Levers are simple machines that can change the force that is produced by increasing or decreasing the distance forces move. Since both sides of the lever do the same work (conservation of energy, remember?) a change in distance is accompanied by an equal but opposite change in force. This means that increasing the distance a force moves decreases the size of the force by an equal factor.
For Example: Doubling the distance is going to cut the force in half.
The distance that the forces move are directly linked, indeed caused, by the length of the lever arms.
We can thus make the direct connection between length of the lever arms, length that the force moves and the size of the force.
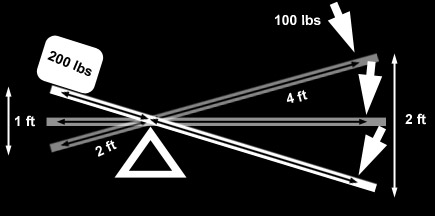
The above image makes the unfortunate choice of using pounds when they should use Newtons to express force. Just replace lbs with Newtons in your mind and it’s fine.
Levers come in three kinds:
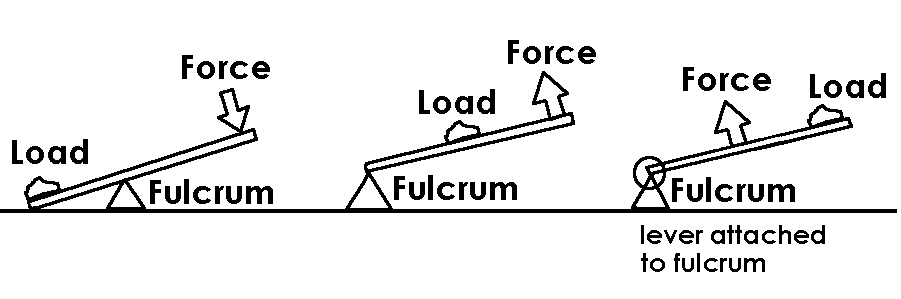
Class I Class II Class III
If you examine these three types of levers you will find that due to where Fin and Fout are located on the lever relative to each other and the fulcrum, each type of lever can produce specific types of MA.
Class I : Since the fulcrum is in the middle it can be closer to Fin or Fout and thus a CLass I lever can produce any kind of MA. Class I levers also always reverse the direction of the force.
Class II: A class II lever has the Load (output) in the middle, which means that it is always closer to the fulcrum and thus always has a shorter Lout (Output Arm). That means that a Class II lever only produces values of MA that are larger than 1.
(asking you to prove that this is so would make for a great question for the upcoming test…)
Class III: Class II levers are the opposite of class II levers insofar that the input and output forces are reversed and thus the value of MA is “reversed” (the proper word is “inverted”). Thus, class III levers can only produce values of MA that are smaller than 1.
Pulleys:
Pulleys work on the same principle as levers by trading and increase in force for a decrease in distance and vice versa. Instead of comparing the length of the lever arms we compare the distance that the load/weight is lifted to the amount of rope/chain we need to pull through the pulley system.
Fixed vs. Movable Pulleys:
Pulleys are either fixed or movable, which means that either they don’t move position or they move with the weight that is being lifted. Pulley systems may contain a mixture of fixed and movable pulleys.
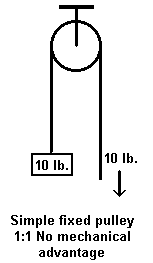
Single Fixed Pulley:
In a single fixed pulley the distance of rope pulled exactly matches the distance the weight is lifted and thus the amount of force also doesn’t change. Ideally we have MA = 1 and only the direction of the force changes, which can be a great advantage in itself.
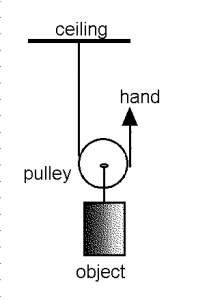
Single Movable Pulley:
A single movable pulley has two rope segments that need to shorten for the weight to rise up. Thus we need to pull twice as much rope through the system compared to how high the pulley is being lifted. This means we have an ideal MA = 2. Another way of looking at it is that half of the weight is held by the rope segment that we are not pulling and thus the ceiling is holding half of the weight.
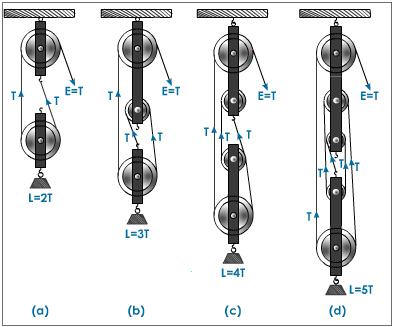
Combination Pulley Systems:
Combination pulley systems have both fixed and movable parts. To figure out the ideal MA of any pulley system simply count rope segments and subtract 1 if you are pulling down (which is the case for each of these pulley systems). Thus the values of MA for these 4 systems are:
a) MA = 3-1 = 2
b) MA = 4-1 = 3
c) MA = 5-1 = 4
d) MA = 6-1 = 5
Example Problem:
We are lifting a heavy workshop door using a pulley system. The door has a weight of 4,000N and we are pulling with 200 N. What is the MA of the pulley?
MA = Fout ÷ Fin = 4,000N ÷ 200 N = 20
The MA of this pulley system is 20.
Side questions: If we lift the door 3m, how much rope do we need to pull through the system?
Enter Friction….. (Part deux):
Until now we have ignored friction in our calculations, but since in reality friction is always present, we can do so no longer. Friction adds an extra amount of force that we need to provide to make the machine parts move. It is thus always an increase of the input force that is the result of friction.
We amend our initial calculation for MA (which we really should have called ideal mechanical advantage IMA) to now calculate real mechanical advantage RMA in the following way:
RMA = Fout ÷ (Fin + friction)
As an example let’s assume that without friction we could lift a 600N weight by using 200N of input on a lever or pulley. The system has an IMA of 600N / 200N = 3.
In reality the machine has an internal friction of 50N that we need to also overcome. Our real input force is thus 250N (not 200N).
The RMA then is:
RMA= 600N / (200N + 50N) = 600N/250N= 2.4
Furthermore, the comparison of RMA to IMA allows us to say something about how efficient the machine is. How much of our actually applied force is returned to us as useful work and how much is wasted in overcoming friction.
2.4/3 = 0.8 or 80%.
Due to friction 20% of our actually applied force is wasted.
Other Machines:
Just like pulleys also used a trade-off between distance and force so do other machines that produce mechanical advantages.
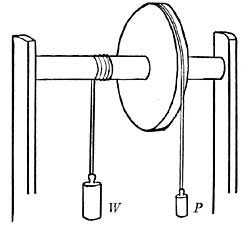
Wheel and axle:
As you can see in the picture, (I hope) a larger weight can be balanced with a smaller weight if the smaller weight is attached to a larger wheel. The mechanical advantage is directly linked (proportional) to the difference in radius of the wheel and axle:
MA = Radius of Wheel / Radius of Axle
Inclined Plane/Ramp:
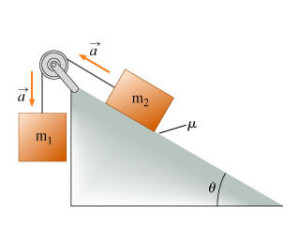
(ignore all the labels please, that’s for high school)
Even though the picture doesn’t show it well, m1 is smaller than m2 meaning that less force is needed to pull a weight up a ramp (ignoring friction which could be considerable) than is necessary to clear lift the object. You can think of it as the ramp holding a portion of the weight that is proportional to the angle of the incline. The steeper the incline the less difference in force there is.
We can calculate MA by:
MA = length or ramp/height of ramp
Please not that by length we mean the longest side of the triangle (the hypotenuse).
Gears:
As you can see, the two gears do not have the same number of teeth. Just like with wheel and axle we have a size difference that is countable. We can calculate MA by simply comparing gear teeth of the driving gear (the input) to the teeth of the driven gear (the output). lets even call them input gear and output gear for convenience.
MA = Teeth of output gear/ Teeth of input gear
In this second picture for example lets say that the smaller gear (22 teeth) is driving the larger gear (60 teeth). Yes I counted because I have nothing better to do with my free time than make up science problems…….
MA = 60/22 = 2.72
We could put it in these terms. The smaller gear needs to turn 2.72 times for on rotation of the larger gear.
We could reverse the two roles and have the larger gear be the input in which case we would get an MA of:
MA = 22/60 = 0.37
Final Design Challenge:
Mousetrap Race cars
Details to follow, but you can check here already:
http://www.youtube.com/watch?v=o3n4RwTxlAk
http://www.youtube.com/watch?v=KWKYNd3IcQc&feature=related